sábado, 13 de dezembro de 2008
Relato de Vinícius
O tempo que nós fizemos o blog, foi legal, porque nós entramos num mundo diferente, o da internet. Para quem não sabia muito, aprendi bastante, me abriu outros caminhos. Espero continuar aprendendo!
quinta-feira, 11 de dezembro de 2008
Relato do Éder
No dia que a professora nos falou da idéia que ela tinha de nós ao invés de fazer trabalhos, constriur blog's, eu pensei pra mim, "ai vem uma baita bobagem e difícil ainda por cima", mas me enganei, porque esse trabalho não foi nem um pouco complicado e não era aquela coisa chata de pesquisar, copiar e entregar os trabalhos no colégio, essa idéia me divertiu bastante e mais importante que isso, eu aprendi muito com esse blog. Eu não gostei de ter repetido de ano em 2007, mas como a professora Grace me falou outro dia, valeu a pena eu ter rodado, porque esse ano eu to bem mais interessado no colégio, e também porque se eu tivesse passado, eu este ano talvez não ia ter aprendido tanto como aprendi. Se tivesse passado teria acabado o colégio muito menos preparado do que estou agora. Ainda não estou tão bem preparado para enfrentar o mercado de trabalho, mas não quero ficar outro ano no colégio para me preparar (heheheh). Eu gostei tanto desse blog que até estou pensando em fazer outro blog, mas com assuntos diferentes. As coisas que eu fiz nesse blog não foram apenas para ganhar nota, foi também por diversão, coloquei coisas nesse blog que não tinham nada a ver com as notas no colégio, tipo: Contador de visitas, marcador de data, link's que vão para os blog's dos meus colegas e da professora Grace, um lugar para procurar musicas (Letras de musicas), etc. Resumindo tudo isso que já falei, foi muito interessante essa experiência que tive esse ano.
quarta-feira, 10 de dezembro de 2008
Geometria Analítica
Vamos agora iniciar uma atividade proposta no blogmat sobre geometria analítica no site da UNIJUI.
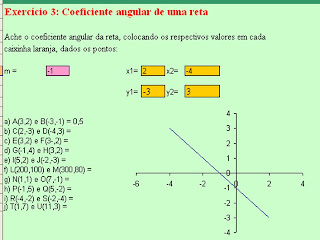
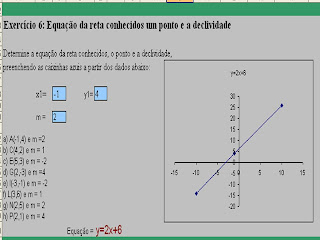
1ª) Quando movimentamos apenas uma reta o seu coeficiente angular e também o seu coeficiente linear mudam de valores.
Quando movimentamos o ponto de intersecção muda o coeficiente linear e também as coordenadas do ponto de intersecção.
2ª) Quando movimentamos o ponto Q observamos que quanto menor o ângulo de inclinação da reta menor o coeficiente angular, ou, quanto maior o ângulo de inclinação da reta o coeficiente angular aumenta. (Para ângulos agudos).
Em relação ao coeficiente linear e o ponto de intersecção da reta com o eixo das ordenadas concluímos que ao movimentarmos a reta ambos têm sempre os mesmos valores.
3ª) O que existe em comum nas equações de duas retas paralelas é que os coeficientes angulares de ambas têm o mesmo valor.
4ª) Sobre retas perpendiculares: sabendo o coeficiente angular de uma reta, para sabermos o coeficiente angular da outra reta é preciso calcular o inverso do simétrico da reta que já tem o valor determinado.
5ª)
1ª) Quando movimentamos apenas uma reta o seu coeficiente angular e também o seu coeficiente linear mudam de valores.
Quando movimentamos o ponto de intersecção muda o coeficiente linear e também as coordenadas do ponto de intersecção.
2ª) Quando movimentamos o ponto Q observamos que quanto menor o ângulo de inclinação da reta menor o coeficiente angular, ou, quanto maior o ângulo de inclinação da reta o coeficiente angular aumenta. (Para ângulos agudos).
Em relação ao coeficiente linear e o ponto de intersecção da reta com o eixo das ordenadas concluímos que ao movimentarmos a reta ambos têm sempre os mesmos valores.
3ª) O que existe em comum nas equações de duas retas paralelas é que os coeficientes angulares de ambas têm o mesmo valor.
4ª) Sobre retas perpendiculares: sabendo o coeficiente angular de uma reta, para sabermos o coeficiente angular da outra reta é preciso calcular o inverso do simétrico da reta que já tem o valor determinado.
5ª)










segunda-feira, 29 de setembro de 2008
Vocês consideram importante que o estudo sobre fractais fosse feito na escola?
Sim.
Já aprendemos algumas coisas sobre Fractais, e gostamos bastante, e por isso seria importante estudarmos essa geometria mais moderna, porque o que a gente aprendeu não foi o bastante, ainda falta muita coisa para aprendermos.
Já aprendemos algumas coisas sobre Fractais, e gostamos bastante, e por isso seria importante estudarmos essa geometria mais moderna, porque o que a gente aprendeu não foi o bastante, ainda falta muita coisa para aprendermos.
Fractais
O que são?
Nos últimos anos, diferentes definições de fractais têm surgido. No entanto, a noção que serviu de fio condutor a todas as definições foi introduzida por Benoît Mandelbrot através do neologismo "Fractal", que surgiu do latino fractus, que significa irregular ou quebrado, como ele próprio disse: "Eu cunhei a palavra fractal do adjectivo em latim fractus. O verbo em latim correspondente frangere significa quebrar: criar fragmentos irregulares, é contudo sabido – e como isto é apropriado para os nossos propósitos! – que, além de significar quebrado ou partido, fractus também significa irregular. Os dois significados estão preservados em fragmento".Os fractais são formas geométricas abstractas de uma beleza incrível, com padrões complexos que se repetem infinitamente, mesmo limitados a uma área finita. Mandelbrot, constatou ainda que todas estas formas e padrões, possuíam algumas características comuns e que havia uma curiosa e interessante relação entre estes objectos e aqueles encontrados na natureza.Um fractal é gerado a partir de uma fórmula matemática, muitas vezes simples, mas que aplicada de forma iterativa, produz resultados fascinantes e impressionantes.Uma 1ª definição, pelo próprio Mandelbrot, diz que: "Um conjunto é dito fractal se a dimensão Hausdorff deste conjunto for maior do que a sua dimensão topológica". Contudo, no decorrer do tempo ficou bastante claro que esta definição era muito restrita, embora apresentasse algumas motivações pertinentes.Existem duas categorias de fractais: os geométricos, que repetem continuamente um modelo padrão e os aleatórios, que são feitos através dos computadores.Além de se apresentarem como formas geométricas, os fractais representam funções reais ou complexas e apresentam determinadas características: auto-semelhança, a dimensionalidade e a complexidade infinita.Uma figura é auto-semelhante se uma parte dela é semelhante a toda a figura. Podemos observar esta característica na curva de Koch.Fractais são objetos geométricos que têm duas características que os diferem dos chamados objetos euclideanos:
1) Auto-similaridade: quando visto de perto ele pode se parecer como se tivesse visto de longe.
2) Não existe forma algébrica de se determinar se um ponto pertence ou não ao fractal, pois sua geração se dá de forma iterativa, isto é, são precisos vários passos para seu desenho e os resultados desses passos têm forte dependência com os resultados dos passos anteriores.
Aqui vão alguns dos mais conhecidos Fractais:
Conjunto de Mandelbrot:

Triângulo de Sierpinski:

Nos últimos anos, diferentes definições de fractais têm surgido. No entanto, a noção que serviu de fio condutor a todas as definições foi introduzida por Benoît Mandelbrot através do neologismo "Fractal", que surgiu do latino fractus, que significa irregular ou quebrado, como ele próprio disse: "Eu cunhei a palavra fractal do adjectivo em latim fractus. O verbo em latim correspondente frangere significa quebrar: criar fragmentos irregulares, é contudo sabido – e como isto é apropriado para os nossos propósitos! – que, além de significar quebrado ou partido, fractus também significa irregular. Os dois significados estão preservados em fragmento".Os fractais são formas geométricas abstractas de uma beleza incrível, com padrões complexos que se repetem infinitamente, mesmo limitados a uma área finita. Mandelbrot, constatou ainda que todas estas formas e padrões, possuíam algumas características comuns e que havia uma curiosa e interessante relação entre estes objectos e aqueles encontrados na natureza.Um fractal é gerado a partir de uma fórmula matemática, muitas vezes simples, mas que aplicada de forma iterativa, produz resultados fascinantes e impressionantes.Uma 1ª definição, pelo próprio Mandelbrot, diz que: "Um conjunto é dito fractal se a dimensão Hausdorff deste conjunto for maior do que a sua dimensão topológica". Contudo, no decorrer do tempo ficou bastante claro que esta definição era muito restrita, embora apresentasse algumas motivações pertinentes.Existem duas categorias de fractais: os geométricos, que repetem continuamente um modelo padrão e os aleatórios, que são feitos através dos computadores.Além de se apresentarem como formas geométricas, os fractais representam funções reais ou complexas e apresentam determinadas características: auto-semelhança, a dimensionalidade e a complexidade infinita.Uma figura é auto-semelhante se uma parte dela é semelhante a toda a figura. Podemos observar esta característica na curva de Koch.Fractais são objetos geométricos que têm duas características que os diferem dos chamados objetos euclideanos:
1) Auto-similaridade: quando visto de perto ele pode se parecer como se tivesse visto de longe.
2) Não existe forma algébrica de se determinar se um ponto pertence ou não ao fractal, pois sua geração se dá de forma iterativa, isto é, são precisos vários passos para seu desenho e os resultados desses passos têm forte dependência com os resultados dos passos anteriores.
Aqui vão alguns dos mais conhecidos Fractais:
Conjunto de Mandelbrot:

Triângulo de Sierpinski:

quinta-feira, 14 de agosto de 2008
Escola Estadual de Ensino Médio Luiz Maria Ferraz - CIEP
O CIEP foi fundado em 1993, e nesta quarta-feira, dia 20 de agosto, estará completando 15 anos. E para comemorarmos esta data será realizada uma semana comemorativa, que será de 13 a 20 de agosto. Quem quiser participar já está convidado.
Parabéns pelo seu Aniversário
"CIEP"
Parabéns pelo seu Aniversário
"CIEP"
Assinar:
Comentários (Atom)




